架构搜索阅读笔记，Beta-Decay Regularization for Differentiable Architecture Search

2024-11-16 | 阅读：次

架构搜索阅读笔记：β-DARTS: Beta-Decay Regularization for Differentiable Architecture Search

最近做了一个量子架构搜索的项目，对相关的神经架构搜索论文做了简单调研，这里做一个简单的记录分享，以备后用。

首先从deepmind提出的DARTS架构相关的研究开始，这次介绍的论文题为《β-DARTS: Beta-Decay Regularization for Differentiable Architecture Search》，由复旦大学、百度、上海人工智能实验室、悉尼大学以及商汤科技视觉组的研究人员共同完成。论文针对神经网络架构搜索（NAS）中的问题，特别是DARTS方法在性能稳定性和泛化能力方面的不足，提出了一个名为Beta-Decay的正则化方法来改进。

核心内容

背景与动机：随着自动设计深层神经网络的能力不断增强，NAS技术受到了越来越多的关注。其中，基于梯度优化的DARTS因其高效性而受到欢迎。然而，DARTS存在两个主要问题：一是对性能崩溃的鲁棒性较弱；二是搜索到的架构在不同数据集上的泛化能力较差。
提出的方法：为了解决上述问题，论文提出了一种简单但有效的正则化方法——Beta-Decay。这种方法能够通过限制激活的架构参数值及其方差过大，从而对DARTS的搜索过程进行正则化处理。此外，还提供了关于为何及如何起作用的理论分析。
实验验证：通过对NAS-Bench-201等基准测试的实验结果表明，所提方法有助于稳定搜索过程，并使搜索到的网络结构更加易于跨数据集迁移。同时，提出的搜索方案展现出较少依赖于训练时间和数据量的良好特性。此外，作者在多种搜索空间和数据集上进行了综合实验，进一步验证了所提方法的有效性。

核心方法 - Beta-Decay 正则化

该论文的方法可以用一行代码来表示，见下图：

图一：β正则化核心方法

从图一可以看到，Beta-decay正则化简单对模型的架构参数进行限制，即对每个架构参数$\beta$施加约束，使其保持在一个较小的范围内。约束条件如下：
$ L_{\text{Beta}} = mean(log(\sum(exp(\beta)))) $
除了该约束外，模型的其他部分与DRARTS完全相同，相比另一正则化方法DARTS-，对比结果见图二：

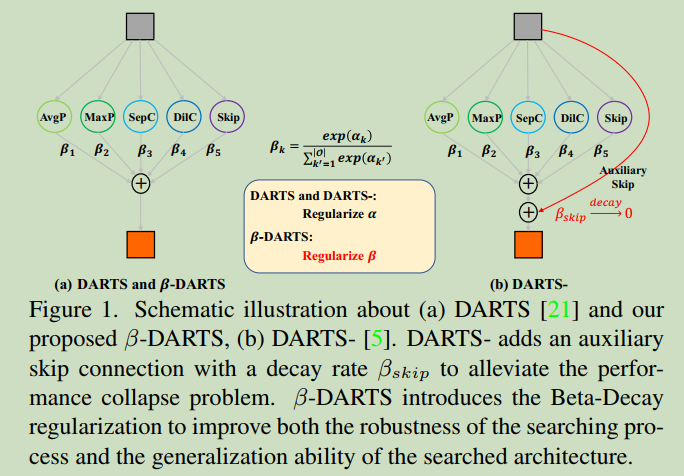
图二：DARTS与β正则化对比

该约束的出发点可以归纳到以下两点：

在DARTS中，每个计算节点包含多个候选操作，通过学习可微分的架构参数β来混合不同操作的输出。为了将离散的操作选择转换成连续的参数优化问题，DARTS采用softmax函数计算出每个操作对应的权重β。针对架构参数β，传统的正则化方法如L2或权重衰减正则化在自适应梯度算法下效果不佳，因为它们会导致每个元素的惩罚相对均匀，部分抵消了正则化的效应。
Beta-Decay正则化直接作用于架构参数的优化过程，通过施加约束以防止激活的架构参数值及其方差变得太大，从而提高搜索过程中架构的稳定性并增强最终架构的泛化能力。

显然，这一方法不仅适用于DARTS，也可以应用于其他基于梯度优化的NAS方法中，可以说提供了一个通用的解决方案。

实验中，Beta-Decay正则化在不牺牲效率的前提下提升了DARTS方法的稳定性和泛化性能，仅在架构参数更新上添加了新的loss项，做了简单修改。

理论分析与证明

尽管方法非常简单，但实验表明了Beta-Decay正则化方法的优势，相比L2和weight decay的对比结果见下图：

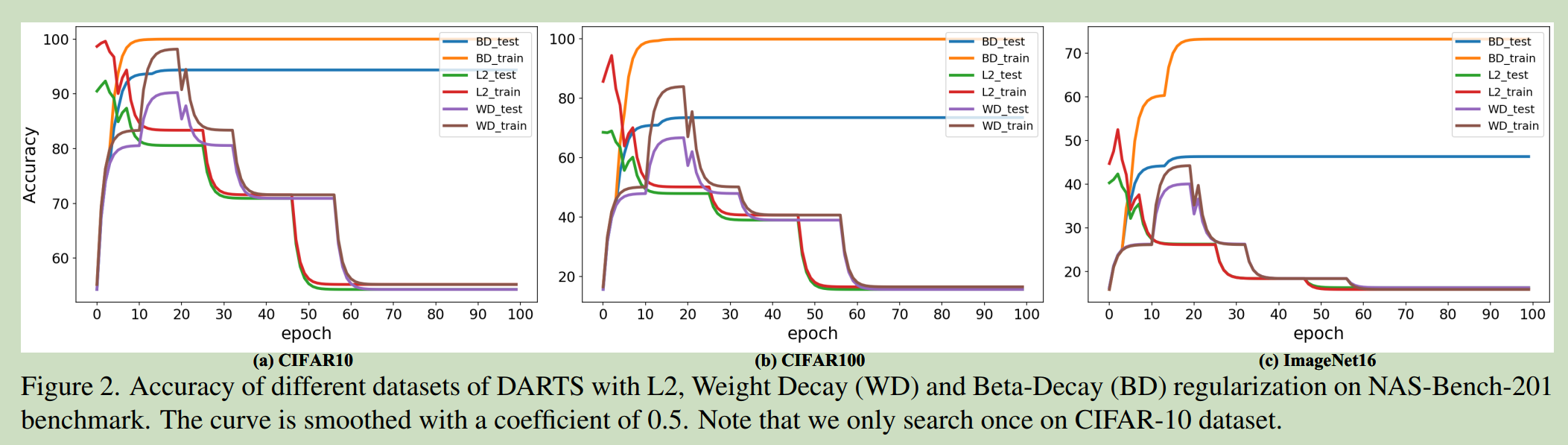
图三：Beta-decay与不同正则化方法的实验结果

理论证明包括两点，分别从鲁棒性和泛化能力两个方面进行证明。

更强的鲁棒性

根据研究工作[2]的结论，超网络（可以理解为DARTS中包含多个子操作的节点）中网络权重$ w $的收敛性严重依赖于架构参数中的skip连接权重$ \beta_{\text{skip}} $。具体来说，假设在搜索空间中有三个操作（卷积、skip连接和无操作），并且训练损失为均方误差（MSE）。当固定架构参数并通过梯度下降优化网络权重时，在一步迭代中，训练损失可以以至少$ 1 - \sigma $的概率降低，降低比率为$ (1 - \eta_w\varphi/4) $，其中$ \eta_w $是相应的学习率，受$ \sigma $约束，且$ \varphi $遵循如下关系：

$ \varphi \propto h^{-2} \sum_{i=0}^{h-1} \left( \beta_{\text{conv}}^{(i,h-1)} \right)^2 \prod_{t=0}^{i-1} \left( \beta_{\text{skip}}^{(t,i)} \right)^2 $

上式中，$ h $是超网的层数。从上面可以看出，$ \varphi $更多地依赖于$ \beta_{\text{skip}} $而不是$ \beta_{\text{conv}} $，这表明当skip连接权重较大时，超网络权重可以更快地收敛。

然而，通过对$ \beta $施加Beta-Decay正则化，可以重新定义$ \varphi $为(同时优化架构参数和网络权重)：

$ \varphi \propto h^{-2} \sum_{i=0}^{h-1} \left( \theta_{\text{conv}}^{(i,h-1)} \beta_{\text{conv}}^{(i,h-1)} \right)^2 \prod_{t=0}^{i-1} \left( \theta_{\text{skip}}^{(i,h-1)} \beta_{\text{skip}}^{(t,i)} \right)^2 $

可以看出，当$ \beta $较大时$ \theta $(即网络权重)变小，当$ \beta $较小时$ \theta $变大。这意味着网络权重的收敛更加依赖于卷积层权重而非skip连接权重。从收敛的角度来看，Beta-Decay正则化限制了skip连接权重的特权，确保了架构参数之间的公平竞争。

更强的泛化能力

参照文献[3]，Lipschitz约束通常用于衡量并改进训练好的深度模型的泛化能力。特别地，假设由深度模型拟合的函数为$ f_w(x) $，其中$ x $是输入。当$ |x_1 - x_2| $非常小时，一个训练良好的模型应该满足以下约束：

$ |f_w(x_1) - f_w(x_2)| \leq C(w) \cdot |x_1 - x_2| $

其中$ C(w) $是Lipschitz常数。该常数越小，训练好的模型对输入扰动就越不敏感，从而具有更好的泛化能力。

进一步地，这种理论可以扩展到可微架构搜索。考虑单层神经网络的情况，多层神经网络可以通过逐步递归分析解决。假设映射函数$ F $选择得当，如使用softmax函数进行归一化，那么Beta-Decay正则化可以帮助最小化架构参数定义的Lipschitz约束，从而确保搜索到的架构具有较好的泛化能力。

综上，通过引入Beta-Decay正则化，可以避免传统正则化方法可能带来的无效惩罚问题，并有效控制架构参数的变化范围，促进搜索过程中架构参数之间的公平竞争，提高搜索结果的稳定性以及网络结构的泛化性能。最关键的，该方法实现起来非常简单，无需对现有代码进行修改，只要在损失函数中添加一个新的loss项即可。